Trabajo colaborativo Fase 2 - Cálculo Diferencial
PREPARATORIA
REGIONAL TEJUPILCO A.C.
INCORPORADA A LA
UNIVERSIDAD AUTÓNOMA DEL ESTADO DE MÉXICO
MATERIA: CÁLCULO
DIFERENCIAL
TRABAJO
COLABORATIVO
FASE
II
EQUIPO
3:
CIPRIANO GARCÍA
ABEL SEBASTIÁN
BARRUETA ARCE ARIAM
MONTSERRAT
CIPRIANO GARCÍA
ABEL SEBASTIÁN
GALVÁN LÓPEZ AB
NEFTALI
LEÓN FERNANDEZ
GISELLE
LÓPEZ LEÓN VALLERY
MARTINEZ DIAZ JAIR
ALEXANDRO
REYEZ SANCHEZ
MIGUEL ANGEL
VENCES PANIAGUA
MITZI GEOVANNA
CATEDRÁTICO:
ING. FRANCISCO BETANZOS CASTILLO
5to Semestre Grupo 2
|
INTRODUCCIÓN
Las funciones están
presentes en la cotidianidad, aunque algunas -por su complejidad- no son
fácilmente relacionadas con los hechos de la vida diaria sino con los ambientes
especializados como en la investigación científica. Algunos procedimientos de
nuestra vida son totalmente descriptibles por fórmulas matemáticas y recordemos
que la descripción de los fenómenos físicos es apenas una aproximación en la
que se usa un modelo matemático.
En la fase dos aprendimos
acerca de la continuidad y su desarrollo en las funciones.
Además de conocer el
concepto, aprendimos a darle solución a la clase de problemas de a
continuación.
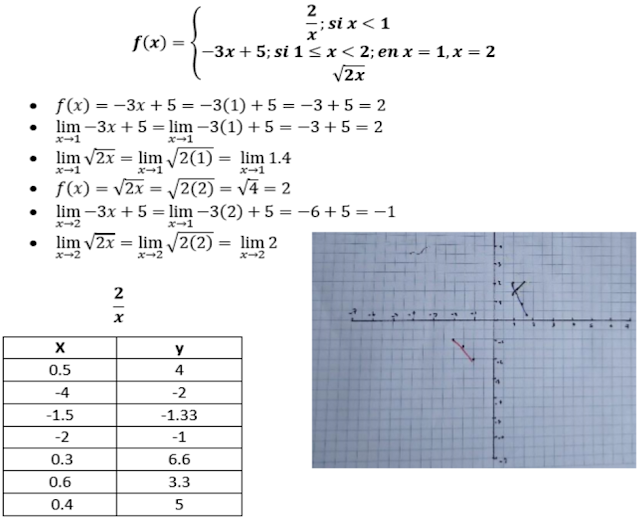
PROBLEMA 1
PROBLEMA 2
PROBLEMA 3
PROBLEMA 4
PROBLEMA 5
CONCLUSIONES
MITZI GEOVANNA
VENCES PANIAGUA
Dentro de este
curso de cálculo hemos visto problemas de funciones continuas y discontinuas,
una función es continua si su gráfica no tiene interrupciones ni saltos, ni
oscilaciones indefinidas, en el sentido que se puede dibujar sin levantar el
lápiz de la hoja de papel; y una función es discontinua si tiene puntos en
los cuales una pequeña variación de la variable independiente produce un salto
en los valores de la variable dependiente. Ejercicios de este tipo de funciones
puede resultar un poco difíciles al momento de realizarlas, pro cuando ya se
tiene noción de cómo realizarlas paso a paso es muy fácil, pero muchos nos
podemos preguntar para qué nos puede servir esto, pues Su introducción nos
permite pasar de la matemática elemental, que comprende Álgebra, Trigonometría,
Geometría plana y del espacio a una Matemática más avanzada, la cual a su vez
comprende el cálculo y sus múltiples aplicaciones.
Algunos
ejemplos podrían ser los siguientes:
- Un arquitecto que se encuentre involucrado en
una gran obra debe trabajar en conjunto con un ingeniero civil, y ambos
deben dominar el cálculo y tener claro el concepto de límite, puesto que
si se va a construir una obra en la que debes realizar aproximaciones con
un margen de error mínimo debes usar límites.
- El cálculo es sin duda una herramienta a la
hora de calcular longitudes, curvas, ángulos y áreas, y siendo el límite
la base del cálculo, vemos la importancia que tiene en la Arquitectura y
en Ingenierías.
- Se puede usar límites para la elaboración de
gráficas que muestren el nivel de producción y el costo de materiales,
para poder generar la mayor ganancia posible: Es decir que el arquitecto
puede usar los límites para hacer un análisis financiero de una obra.
- Pero no solo en la Arquitectura se emplea el
uso del cálculo y los límites, sino también en otras áreas y ciencias, por
ejemplo una función continua proporciona la expresión matemática en las
leyes que rigen el movimiento de los cuerpos s= f (t) que expresan la
dependencia de la distancia s respecto del tiempo t, puesto que el tiempo
y la distancia son continuos.
ABEL SEBASTIÁN
CIPRIANO GARCÍA
Fue ahora en esta parte donde dimos seguimiento al
conocimiento sobre las funciones y límites, pero en este caso pasamos a lo que
son la continuidad de funciones.
Como vimos previamente, una función f(x) es
contínua en el punto XER Si cumple con las condiciones: f(x) debe estar
definida y su límite existe.
Los ejercicios que se resolvieron en clase
sirvieron para darnos una noción o introducción a los que se resolvieron
en esta fase 2 del proyecto, aunque si fue un poco difícil, por el aumento de
dificultad que se les iba dando.
A mi percepción, en la naturaleza y en nuestra vida
diaria aparecen numerosos fenómenos que tienen un comportamiento continuo.
Entiendo como un ejemplo el siguiente: el crecimiento de una planta es
continuo, el desplazamiento de un vehículo o el volumen del agua que fluye de
un recipiente. O en su caso contrario, que son las discontinuidades, se
encuentra lo que es la corriente eléctrica.
Muchos procesos que observamos diariamente son
continuos como pudimos notar en los ejemplos anteriores. Se entiende en
primer plano a la continuidad en el cálculo como graficar algo sin
interrupciones o secciones cortadas. De la misma manera, se puede decir que una
función es discontinua en un punto, si se debe interrumpir el trazo en el papel
para obtener la gráfica de la función a ambos lados del punto indicado.
La definición matemática de continuidad responde al
significado de la palabra continuidad en el lenguaje cotidiano. Se puede pensar
que un proceso continuo tiene lugar gradualmente, sin interrupciones ni cambios
abruptos.
Cabe resaltar que para la realización de este
trabajo, fue muy necesaria la colaboración de todos los integrantes, y ayuda de
otros compañeros externos, aunque la mayoría se pudo resolver gracias a los
conocimientos que adquirimos a lo largo del módulo, la noción fue muy útil, y
nos será de gran apoyo para continuar con el curso de cálculo diferencial.
ARIAM MONSERRAT
BARRUETA ARCE
En la fase dos aprendimos acerca de la continuidad,
su historia y su desarrollo en las funciones. El cálculo diferencial e integral
surgió en el siglo XVII, el concepto de función vino a conocerse un siglo
después, y el límite, entendido de una manera formal y rigurosa, solo a finales
del siglo XIX, lo cual difiere de la forma como se presenta actualmente el
cálculo, en donde primero se enseñan funciones, luego límites y finalmente
derivadas o integrales.
Además de conocer el concepto y un poco de su
historia, aprendimos a darle solución a esta clase de problemas.
Por Ejemplo:
F (x)= 5/x 4 -16
La función es continua en todos los puntos de su
dominio.
D = R− {−2,2}
La función tiene dos puntos de discontinuidad en x
= −2 y x = 2.
GISELLE LEÓN
FERNÁNDEZ
Las funciones en la vida cotidiana Las funciones
están presentes en la cotidianidad, aunque algunas -por su complejidad- no son
fácilmente relacionadas con los hechos de la vida diaria sino con los ambientes
especializados como en la investigación científica. Algunos procedimientos de
nuestra vida son totalmente descriptibles por fórmulas matemáticas y recordemos
que la descripción de los fenómenos físicos es apenas una aproximación en la
que se usa un modelo matemático. Sin embargo, por otro lado, cualquier lugar
del universo, por ende en la naturaleza y en la vida diaria, aparecen numerosos
fenómenos que tienen un comportamiento continuo. Por ejemplo: el crecimiento de
una planta es continuo, el desplazamiento de un vehículo o el volumen del agua
que fluye de un recipiente, el movimiento planetario y una infinidad de otros
eventos. Aunque también se presentan discontinuidades en muchas situaciones
como: las corrientes eléctricas, la cantidad de lluvia que cae, la fuerza del
viento y otros fenómenos.
Una línea continua es algo que no se corta que
tiene que seguir, las aplicaciones de la continuidad como las funciones en si
es algo más complejo, por eso la siguiente investigación da a conocer algunos
conceptos básicos y ejemplos de este tipo de función así como de sus
aplicaciones. Se verán algunos ejemplos de la discontinuidad también.
Finalmente se aprenderá a graficar y resolver ejercicios basándose en los
conceptos que se darán a conocer.
La continuidad es una hipótesis fundamental, no
solo en el Cálculo, sino en la Física Clásica, es parte de la definición básica
de sistema homogéneo y lineal, sería imposible derivar e integrar sin este
concepto, y simplemente seguiríamos viviendo con la tecnología del siglo XVII
si nunca se hubiese definido ese concepto; de hecho, la sola idea de que la
energía es discontinua fue el motor que provoco todo el desarrollo de la Física
Moderna.
VALLERY GÓMEZ
LEÓN
Continuidad es un término que se refiere al vínculo
que mantienen aquellas cosas que están, de alguna forma, en continuo. Hace un
tiempo, el concepto también se empleaba como sinónimo de continuación, aunque
hoy este uso es algo arcaico.
En matemáticas, una función continua es aquella
para la cual, intuitivamente, para puntos cercanos del dominio se producen
pequeñas variaciones en los valores de la función. Si la función no es
continua, se dice que es discontinua. Una función continua de \R en \R es
aquella cuya gráfica puede dibujarse sin levantar el lápiz del papel (más
formalmente su grafo es un conjunto conexo).
La continuidad de funciones es uno de los conceptos
principales del análisis matemático y de la topología. El artículo describe
principalmente la continuidad de funciones reales de una variable real.
Una función es continua si su gráfica puede
dibujarse de un sólo trazo.
Intuitivamente, la continuidad significa que un
pequeño cambio en la variable x implica sólo un pequeño cambio en el valor de
f(x), es decir, la gráfica consiste de un sólo trozo de curva.
En contraste, una gráfica como la de la función
f(x) = sgn x (signo de x) que consiste de pedazos de curva separados por un
vacío en una abscisa exhibe allí una discontinuidad.
La continuidad de la función f(x) para un valor a
significa que f(x) difiere arbitrariamente poco del valor f(a) cuando x está
suficientemente cerca de a.
Expresemos esto en términos del concepto de límite.
JAIR ALEXANDRO
MARTÍNEZ DÍAZ
En la actualidad el alumno de nivel medio superior
se ah dicho por lo menos una sola vez que no saben o no creen que vayan a
ocupar las matemáticas y mucho menos las funciones o los límites y me parece
una excelente idea este proyecto ya que ahora si como dicen dar con guante
blanco porque se da ah conocer a muchos alumnos que realmente si las vamos a
ocupar ya sea para los negocios o con solo pensar en la posibilidad de que un
acontecimiento suceda ya está en uso los límites talvez no como su concepto en
sí pero está presente así que podemos decir que es un proyecto muy bien
planeado pero para eso debemos saber bien que son los límites las funciones o
tan siquiera que es calculo diferencial, por el tiempo de clases y por estudio
propio puedo decir que
Límites es
límite es una magnitud a la que se acercan progresivamente
los términos de una secuencia infinita de magnitudes expresa la
tendencia de una función o de una sucesión mientras sus parámetros se aproximan
a un cierto valor y ya una definición informal del límite matemático indica que
el límite de una función f(x) es T cuando x tiende a s, siempre que se puede
hallar para cada ocasión un x cerca de s de manera tal que el valor de f(x) sea
tan cercano a T como se pretenda.
Y la función es
que una magnitud es función de otra si el valor de
la primera depende del valor de la segunda. Por ejemplo el área A de un círculo
es función de su radio r (el valor del área es proporcional al cuadrado del
radio, A = π·r2). Del mismo modo, la duración T de un viaje en tren entre dos
ciudades separadas por una distancia d de 150 km depende de la velocidad v a la
que se desplace el tren (la duración es inversamente proporcional a la
velocidad, d / v). A la primera magnitud (el área, la duración) se la denomina
variable dependiente, y la magnitud de la que depende (el radio y la velocidad)
es la variable independiente.
FUENTES
CONSULTADAS
Scientific
American, What is Mathematical Limit?. Disponible en:
http://www.scientificamerican.com/article/what-is-a-mathematical-limit/
Quick and Dirty
Tips. Whats Is a Mathematical Limit? Disponible
en: http://www.quickanddirtytips.com/education/math/what-is-a-mathematical-limit?page=1
Bogotá, B. V. (2018). bachilleratoenlinea.com.
Obtenido de https://bachilleratoenlinea.com/educar/mod/lesson/view.php?id=2497
chrismartinez211996. (23 de Noviembre de
2014). LÍMITES, CONTINUIDAD Y SU APLICACIÓN EN LA ARQUITECTURA.
Obtenido de https://chrismart211996.wordpress.com/2014/11/23/limites-continuidad-y-su-aplicacion-en-la-arquitectura/
EcuRed. (Semtiembre de 2018). EcuRed
conocimiento con todos y para todos. Obtenido de
https://www.ecured.cu/Funciones_continuas












Comentarios
Publicar un comentario